Measuring the knot of degeneracies and eigenvalue braids near a third-order exceptional point
Y. S. S. Patil, J. Höller, P. A. Henry, C. Guria, Y. Zhang, L. Jiang, N. Kralj, N. Read, J. G. E. Harris
Nature 607, 271-275 (2022)
arXiv:2112.00157 (2021)
-
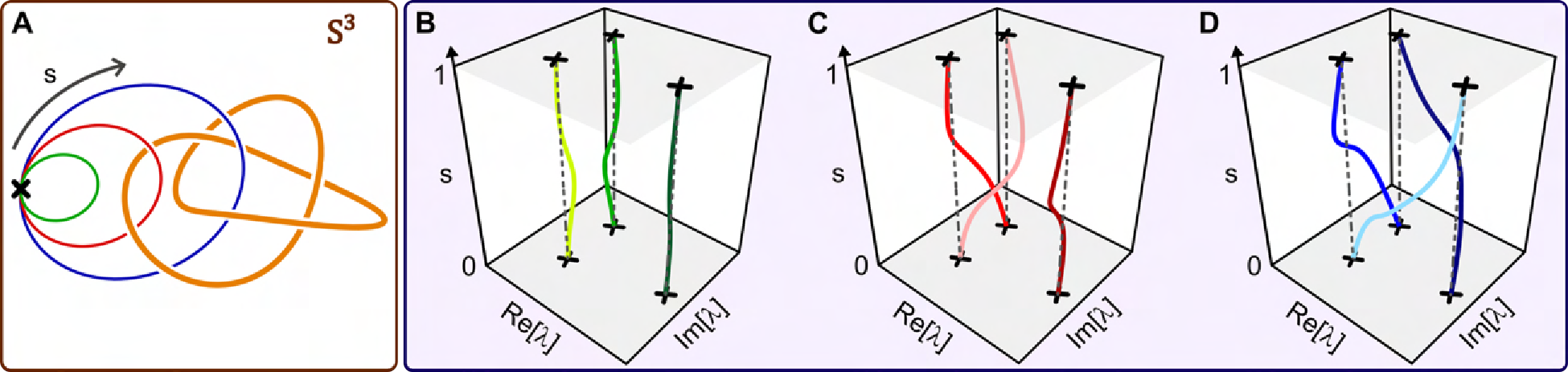
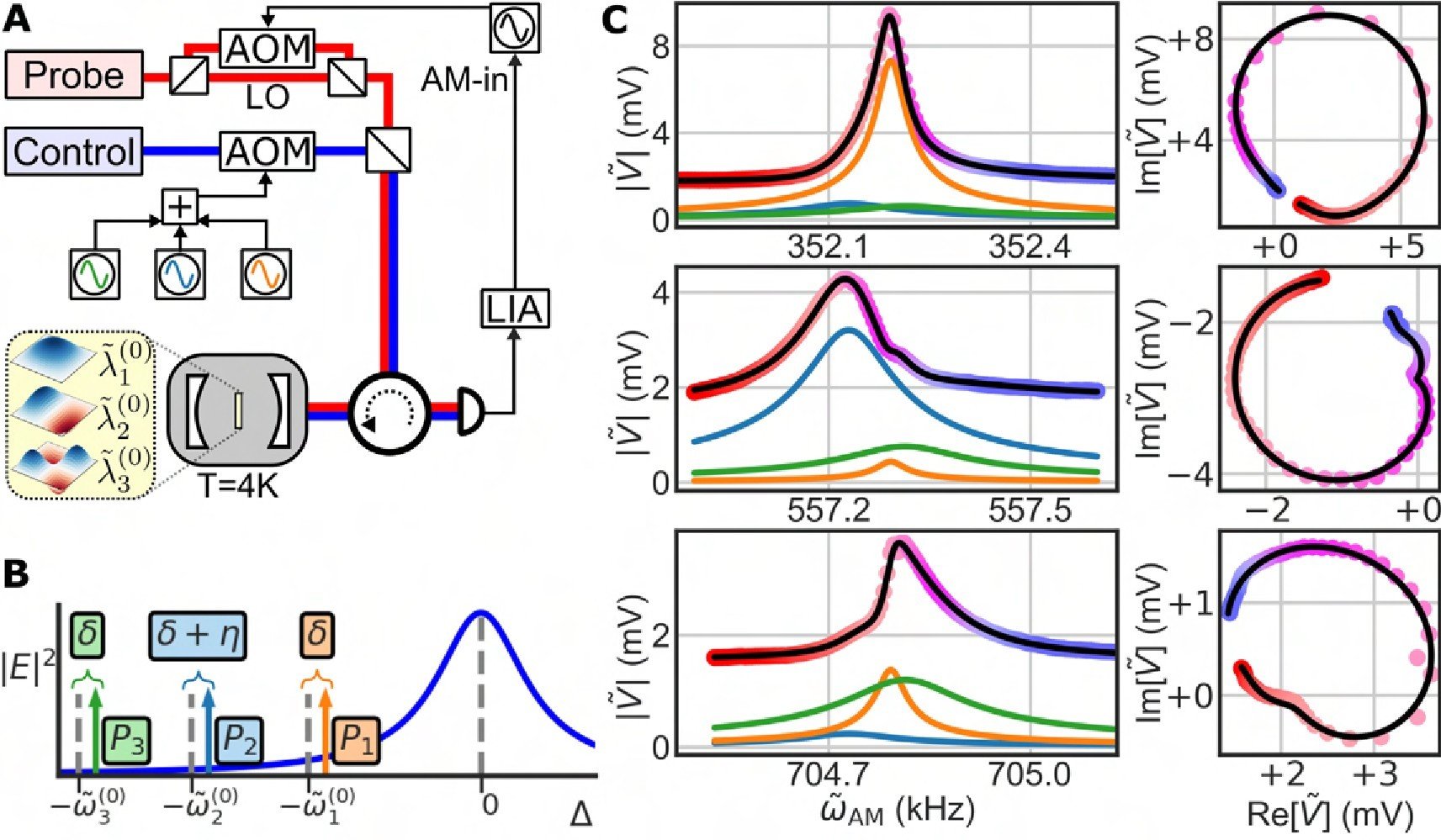
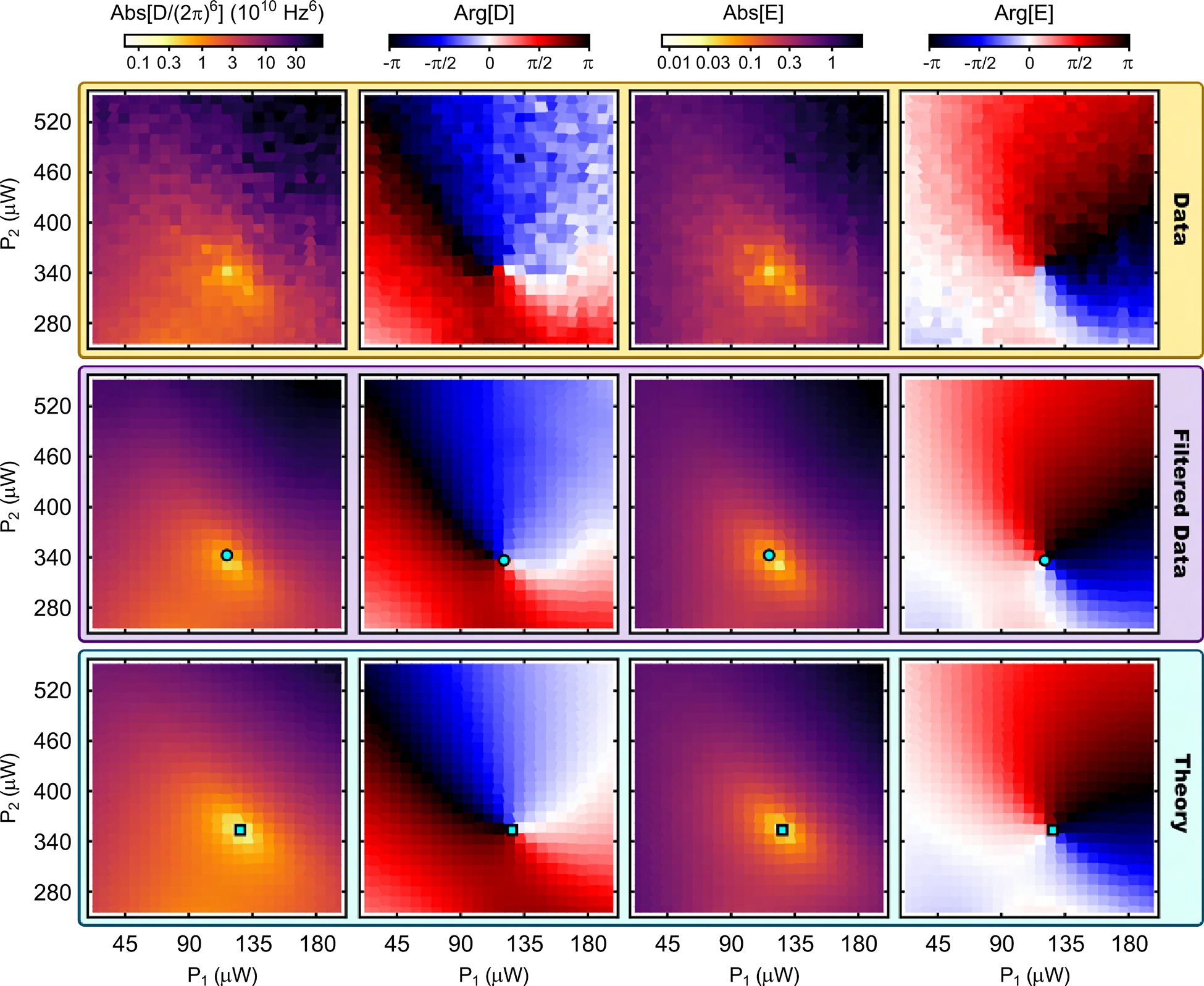
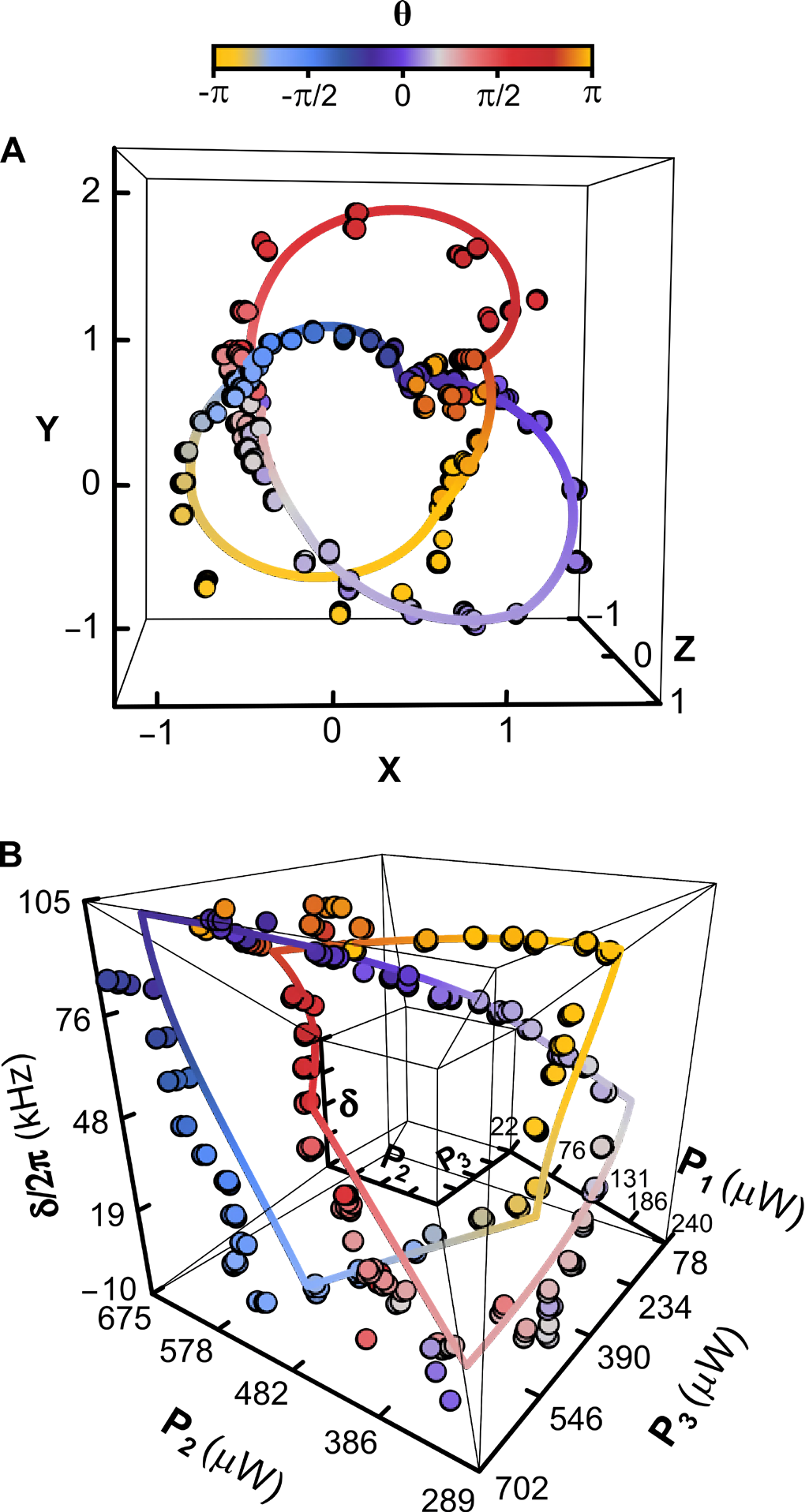
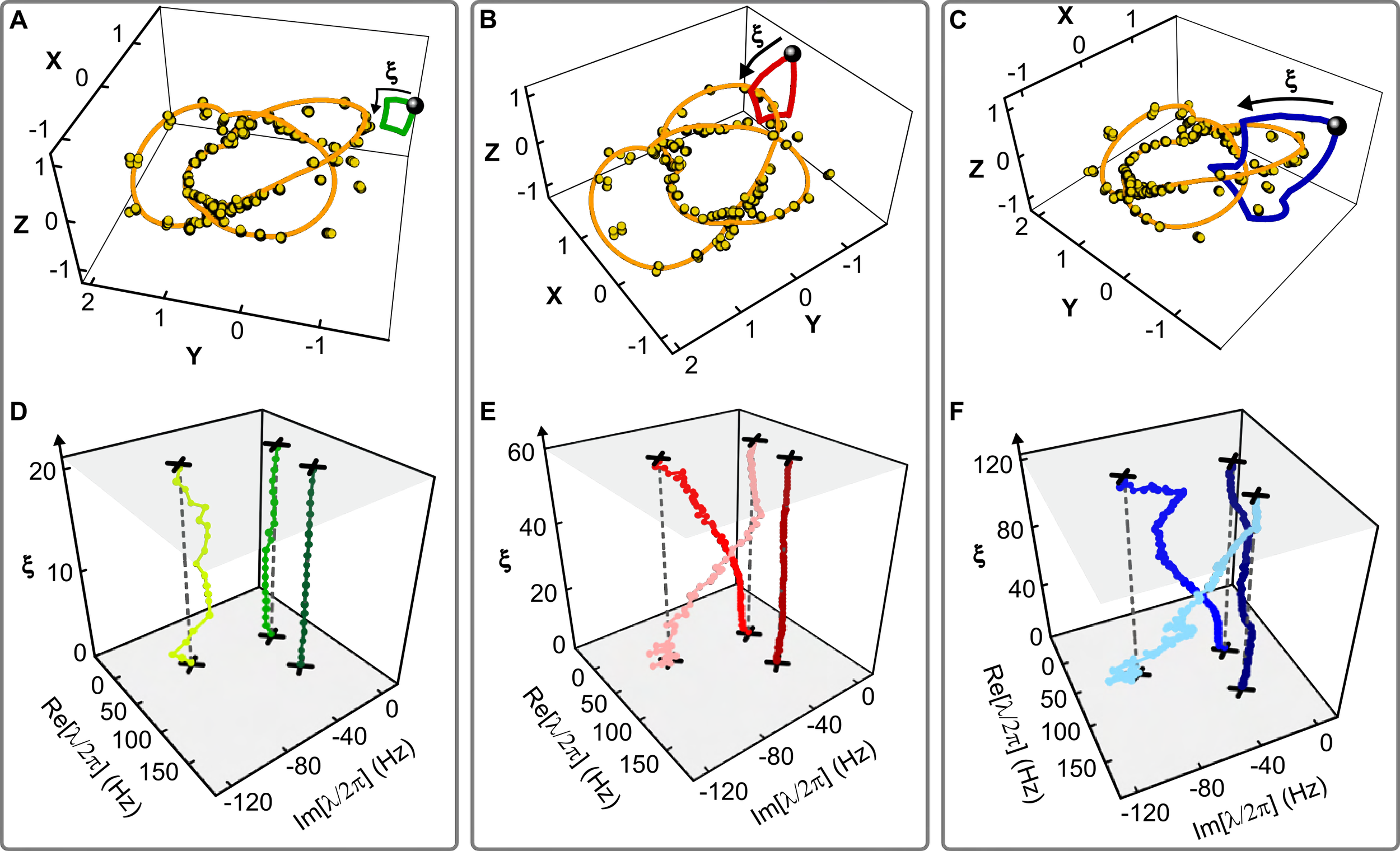
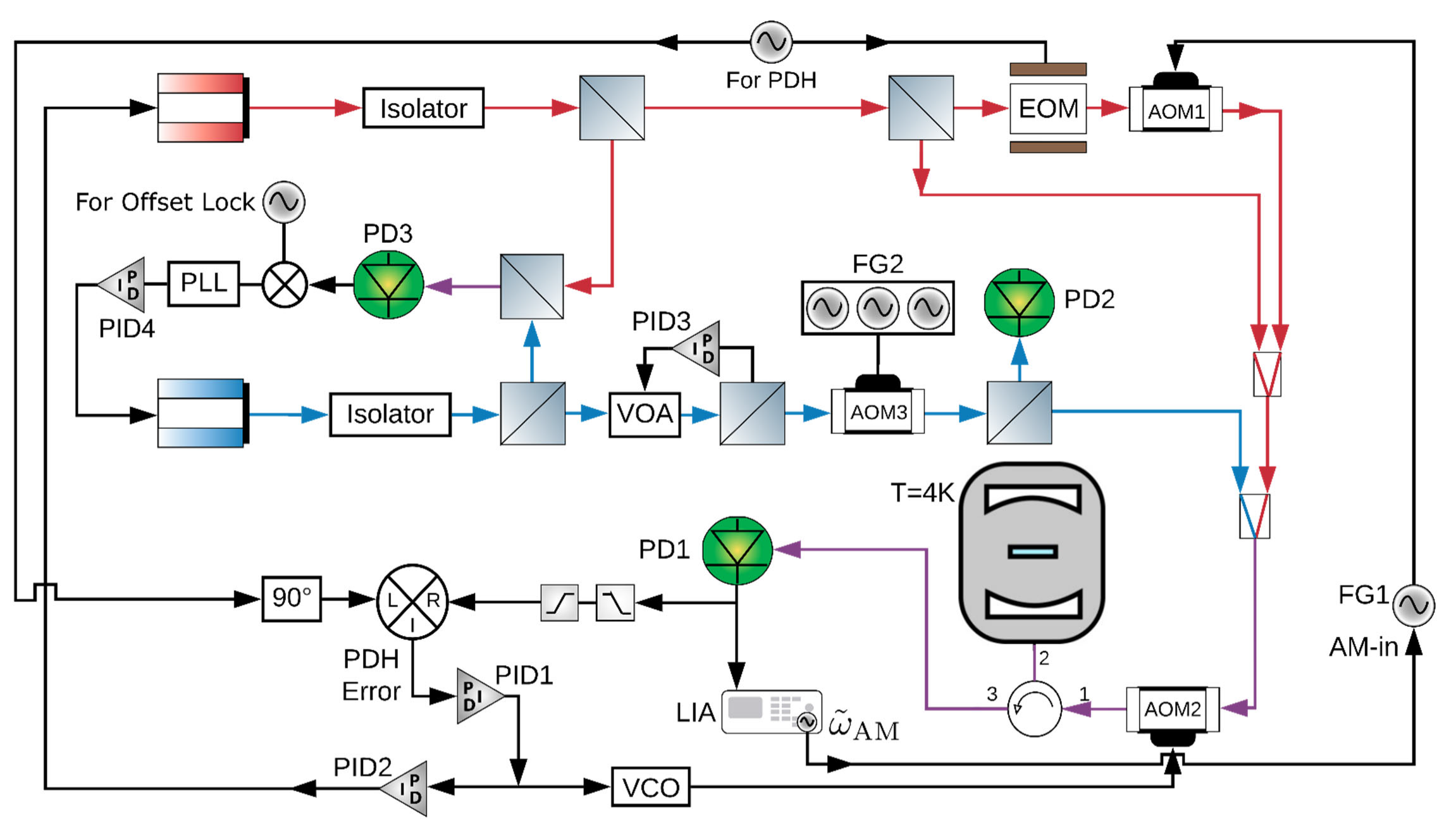
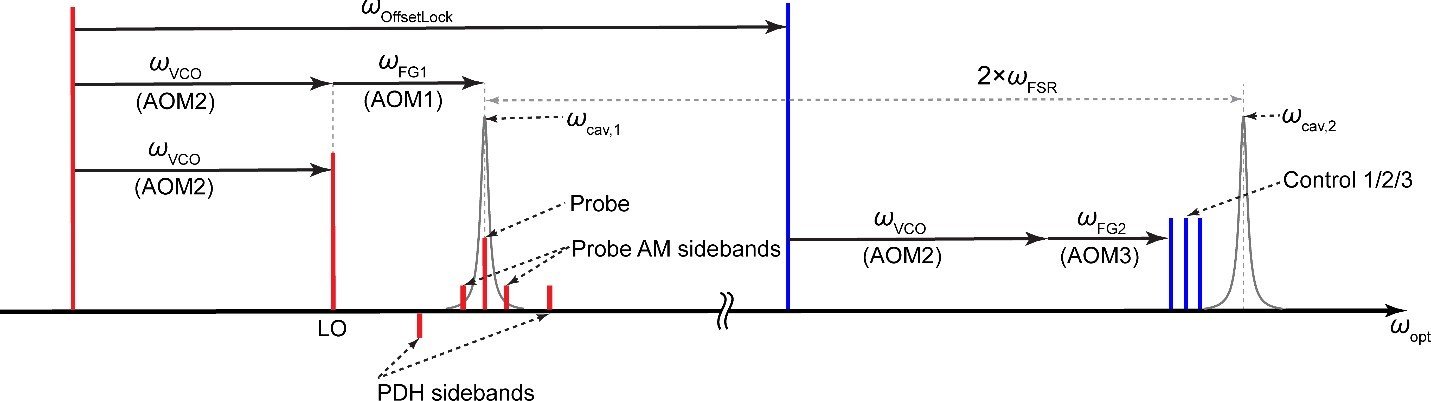
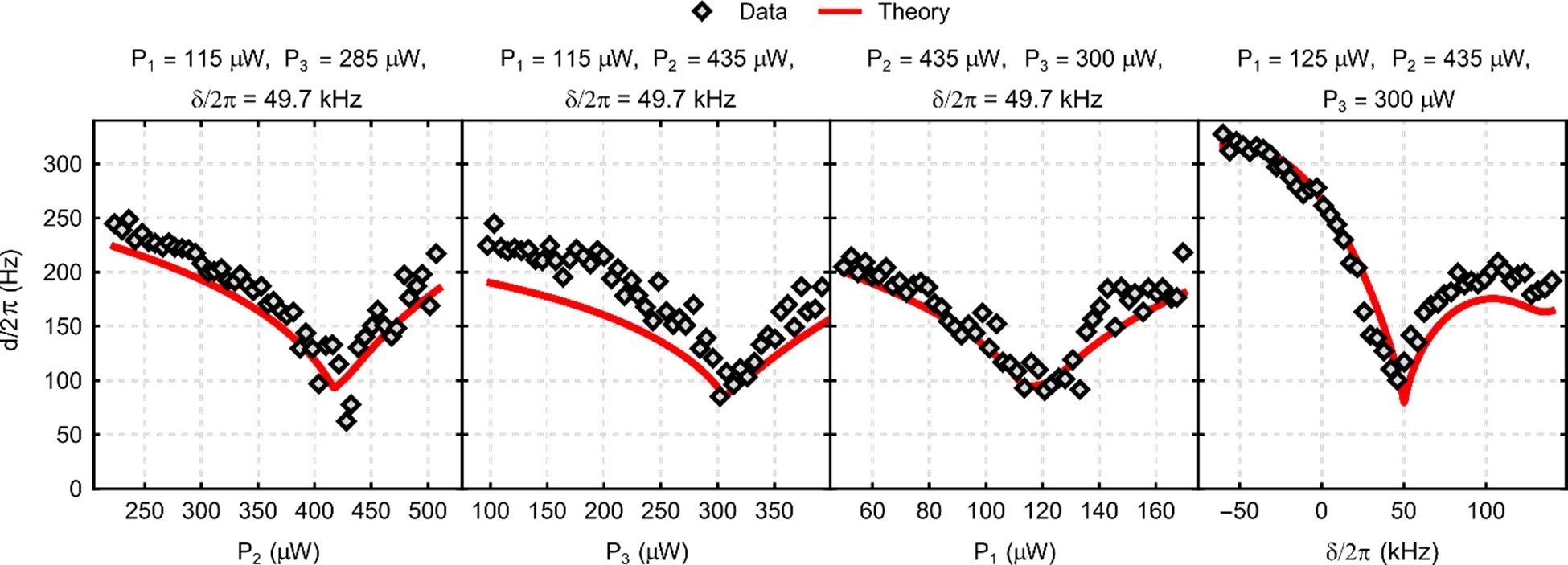
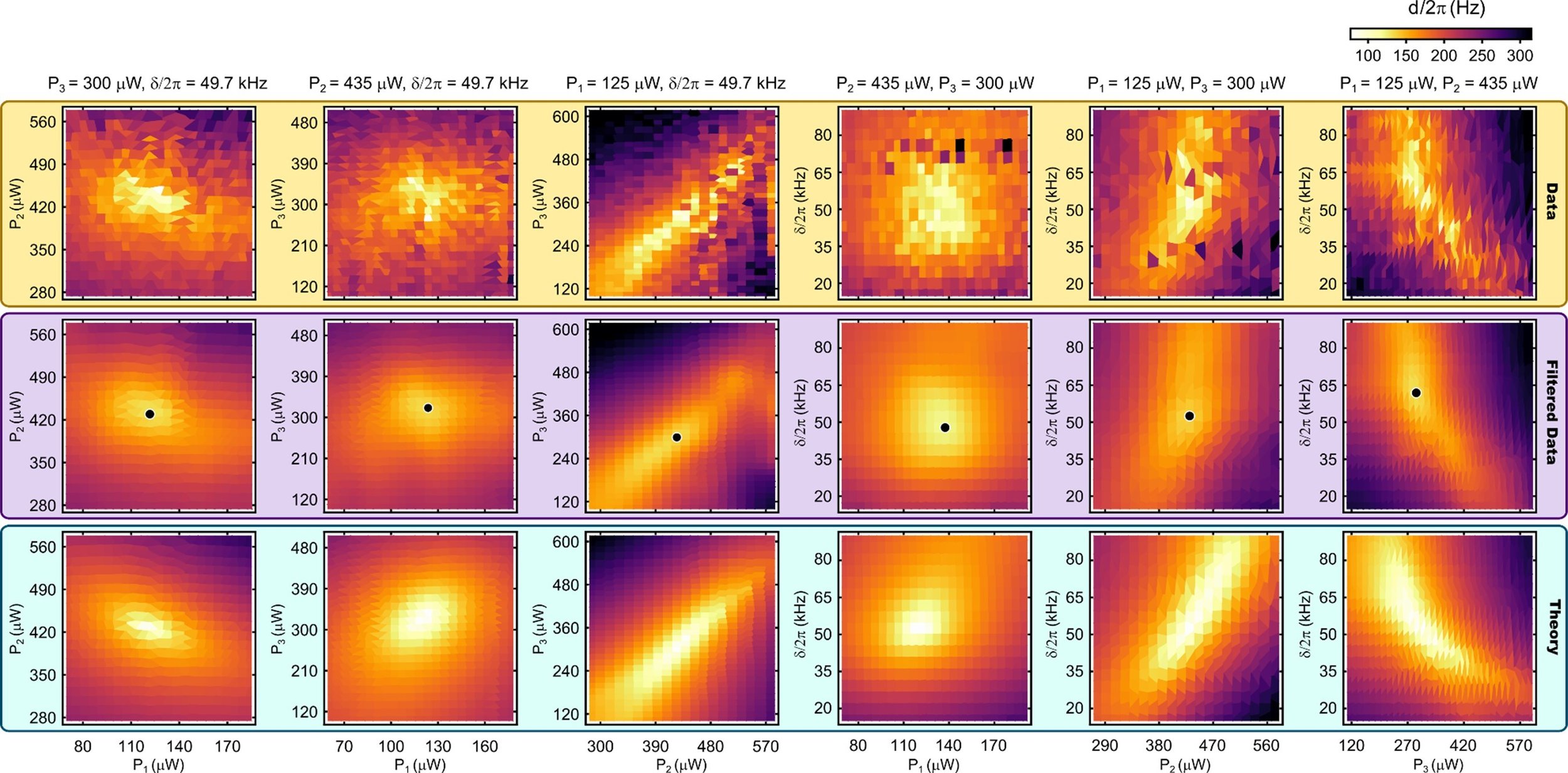
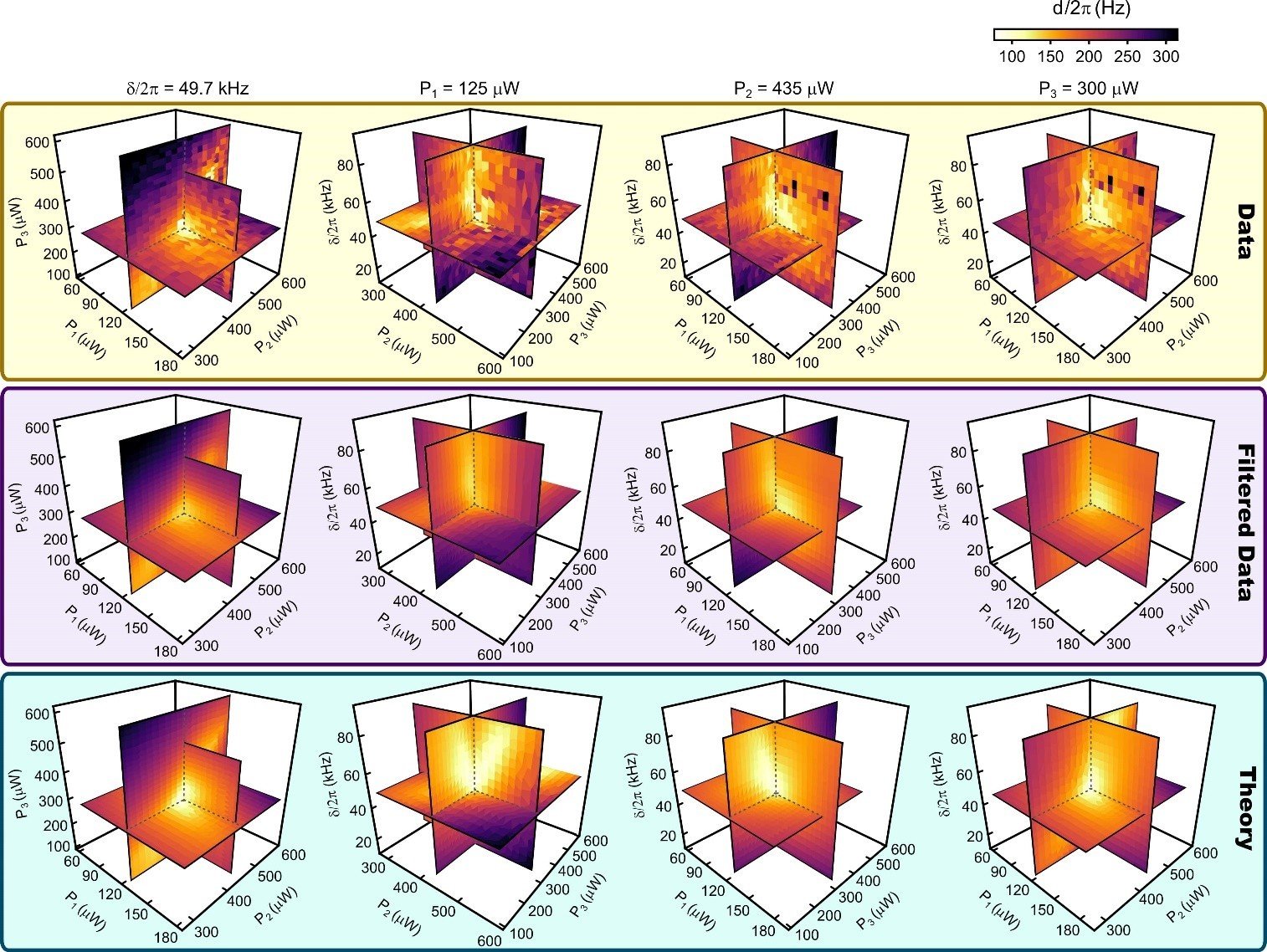
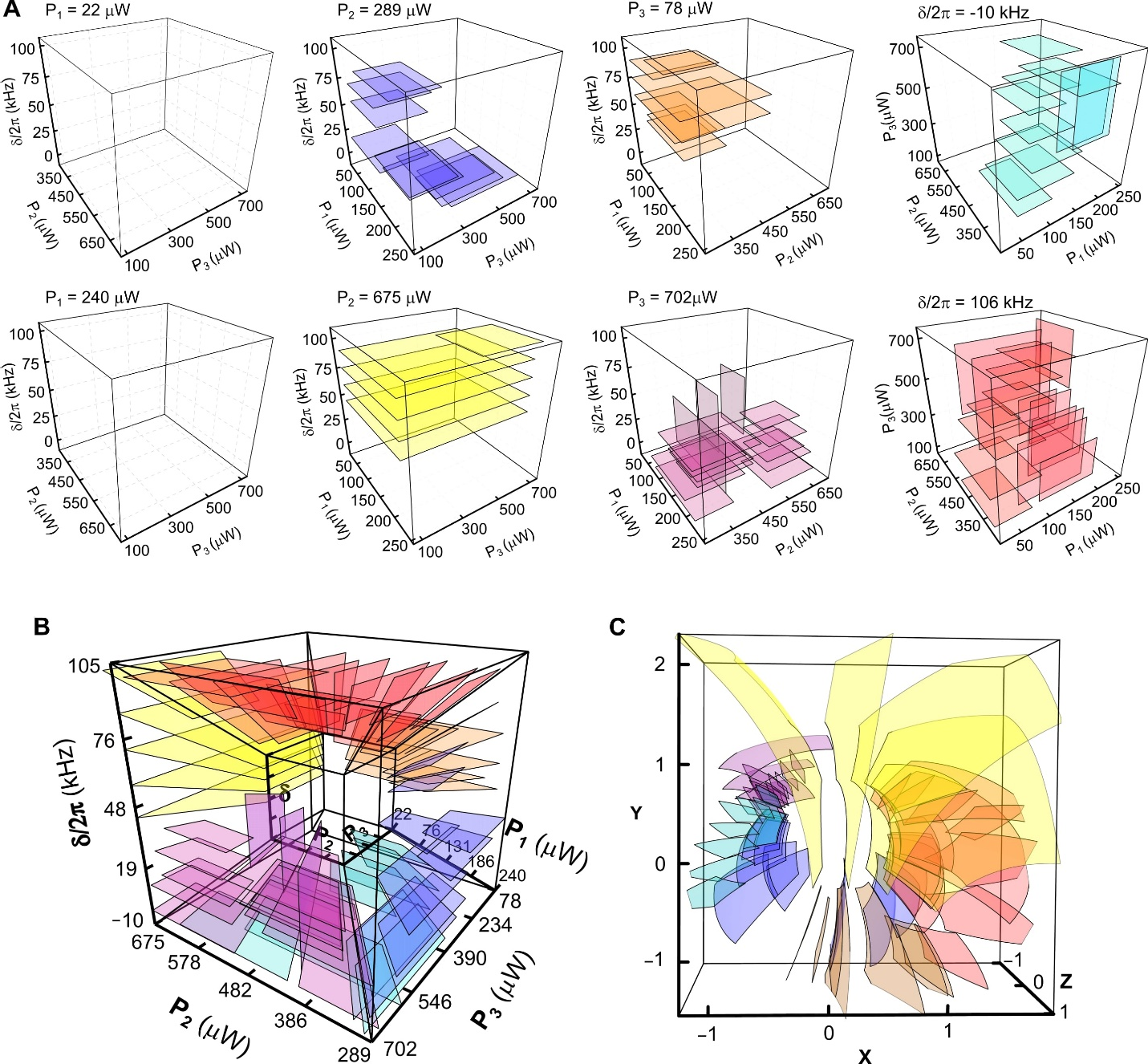
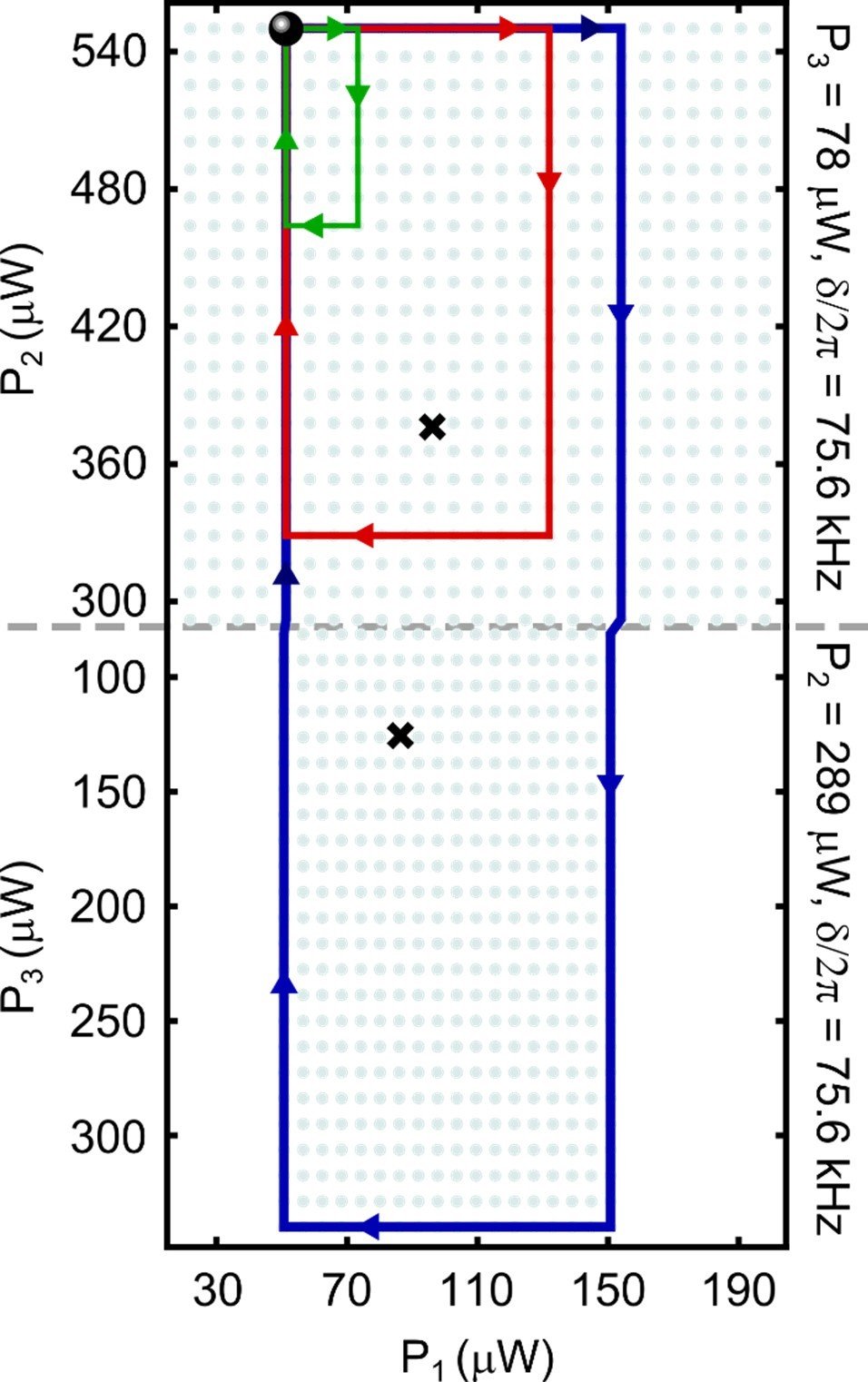
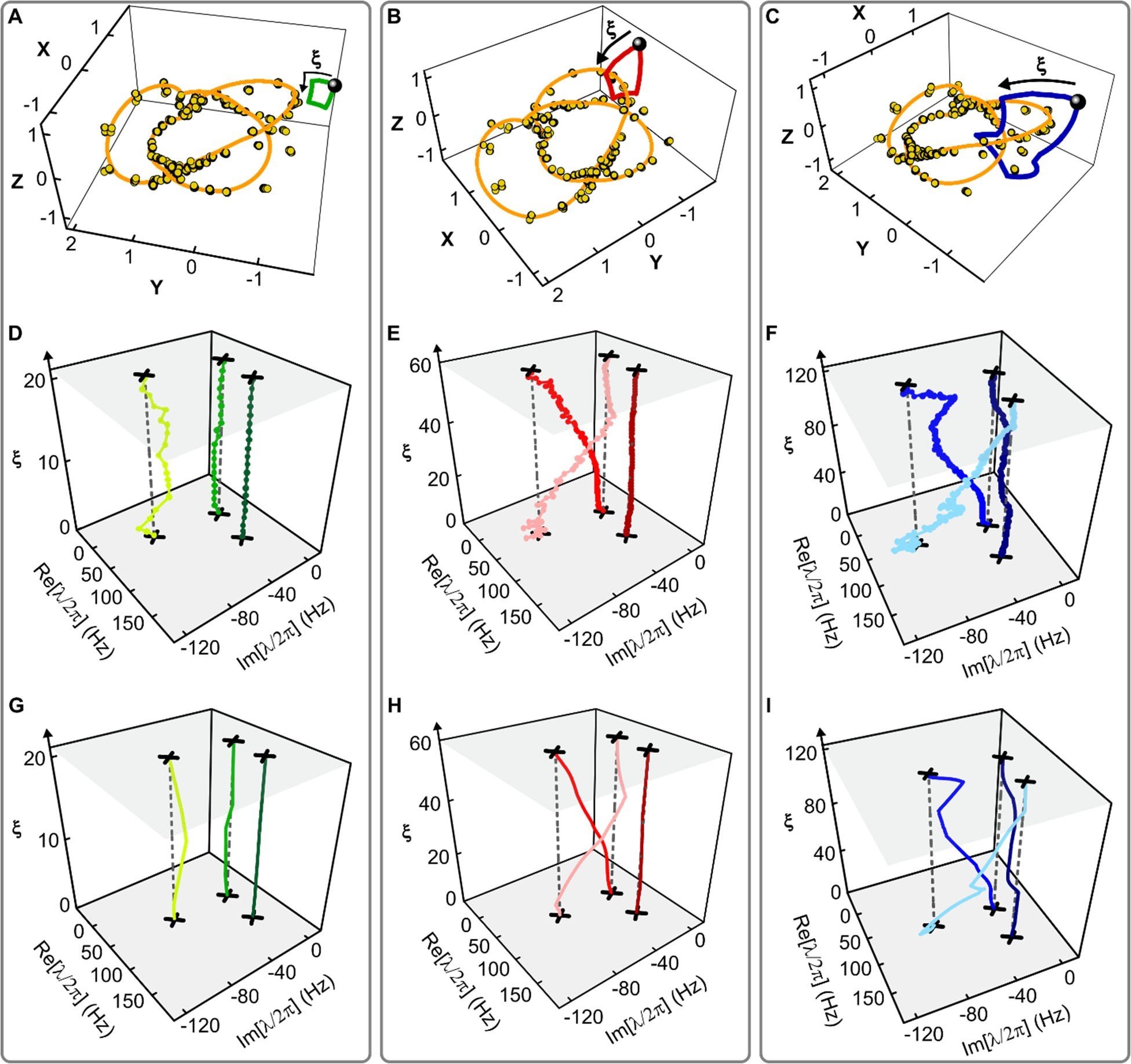
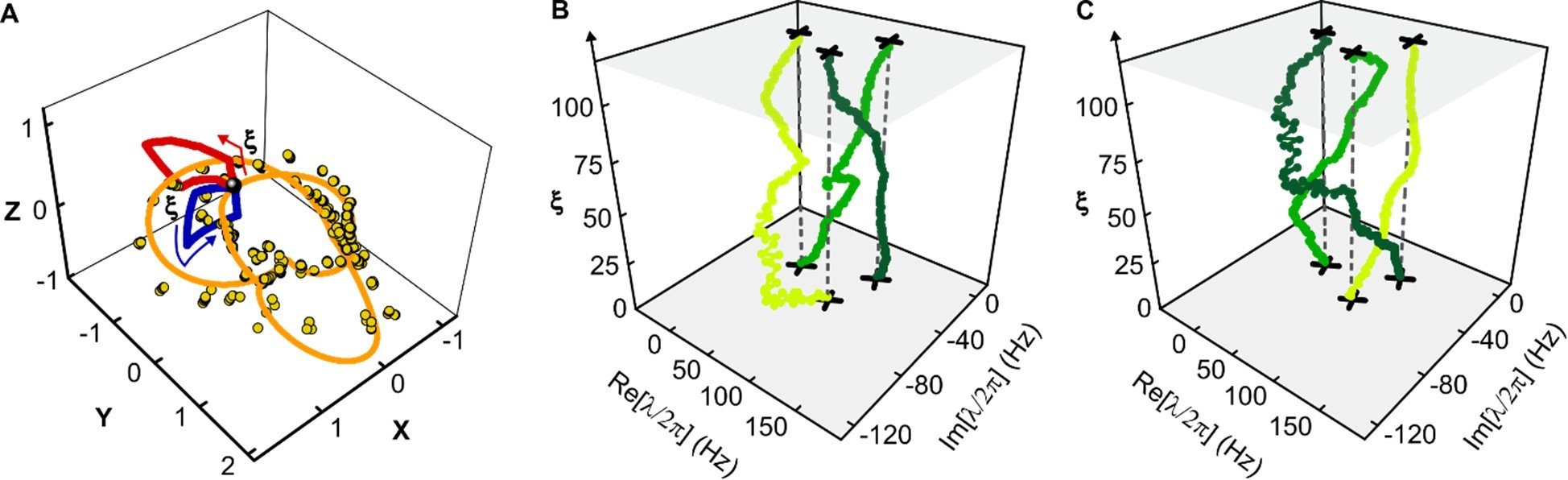
When a system of $N$ coupled oscillators is tuned by varying its external control parameters around a closed path (i.e., a “control loop”), the system’s spectrum of eigenfrequencies must return to itself. In Hermitian systems this return is trivial, as each eigenfrequency returns to its original value. However, in non-Hermitian systems, where the eigenfrequencies are complex, the spectrum may return to itself in a topologically non-trivial manner, a phenomenon known as spectral flow. The spectral flow is determined by how the control loop encircles degeneracies, and for $N=2$ this relationship is well-understood. Here we extend this description to arbitrary $N$. We show that control loops generically produce braids of eigenfrequencies, and that for $N>2$ these braids’ non-commutativity reflects the non-trivial geometry of the space of degeneracies. We demonstrate these features experimentally for $N=3$ using a cavity optomechanical system whose tunability gives access to a third-order exceptional point and all of the spectra in its neighborhood.